Clase 19: Scipy y computación numérica¶

En esta clase revisaremos el trabajo, la librería scipy.

Scipy¶

La librería scipy es una librería de computación científica que utiliza numpy. Nos va a permitir realizar optimización, procesos estadísticos, interpolación, procesamiento de imágenes, integración, entre otros.

Álgebra lineal¶

Para operaciones de álgebra lineal podemos ocupar el módulo linag.

#1. Determinante de una matriz
import numpy as np
from scipy import linalg
arr = np.array([[1, 2],
               [3, 4]])
linalg.det(arr)

-2.0

arr = np.array([[3, 2],
                [6, 4]])

linalg.det(arr)

0.0

#2. Inversa de una matriz
linalg.inv(arr)
# calcular la inversa de una matriz singular (su determinante es cero) generará un error

---------------------------------------------------------------------------
LinAlgError                               Traceback (most recent call last)
<ipython-input-3-317de499420c> in <module>
      1 #2. Inversa de una matriz
----> 2 linalg.inv(arr)
      3 # calcular la inversa de una matriz singular (su determinante es cero) generará un error

~/miniconda3/lib/python3.9/site-packages/scipy/linalg/basic.py in inv(a, overwrite_a, check_finite)
    966         inv_a, info = getri(lu, piv, lwork=lwork, overwrite_lu=1)
    967     if info > 0:
--> 968         raise LinAlgError("singular matrix")
    969     if info < 0:
    970         raise ValueError('illegal value in %d-th argument of internal '

LinAlgError: singular matrix

arr = np.array([[1, 2],
               [3, 4]])
linalg.inv(arr)

array([[-2. ,  1. ],
       [ 1.5, -0.5]])

Optimización¶

Podemos ocupar el módulo optimize para encontrar el mínimo (máximo) de una función (escalares o multidimensional).

from scipy import optimize
import matplotlib.pyplot as plt

def f(x):
    return x**2 + 10*np.sin(x)

x = np.arange(-10, 10, 0.1)
plt.plot(x, f(x)) 
plt.show() 

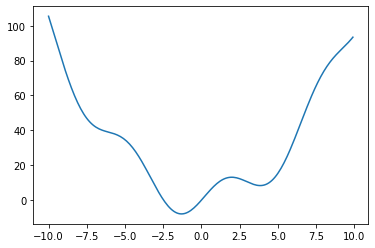
Mínimo global: corresponde al valor mínimo en el dominio de la función. Mínimo local: corresponde al valor mínimo en una región particular de la curva.

En el ejemplo tenemos un mínimo local y un mínimo global. Mediante un algoritmo de scipy podemos encontrar estos valores, por ejemplo podemos usar la función fmin_bfgs (método BFGS) para encontrar el mínimo.

#Usamos el módigo optmize, la función fmin_bfgs
#La sintaxis es fmin_bfgs(función a optimizar, valor inicial)
opt = optimize.fmin_bfgs(f, 0)
print(opt)
#El resultado nos entrega: 
#1) Valor de la función evaluada en el punto mínimo
#2) Número de iteraciones que se demoró en encontrar el mínimo
#3) Número de evaluaciones de la función
#4) Número de evaluaciones del gradiente
#5) Parámetro que minimiza la función

Optimization terminated successfully.
         Current function value: -7.945823
         Iterations: 5
         Function evaluations: 12
         Gradient evaluations: 6
[-1.30644012]

Por la naturaleza del método podemos quedar en el mínimo local si no partimos del “lado correcto”

optimize.fmin_bfgs(f, 3)

Optimization terminated successfully.
         Current function value: 8.315586
         Iterations: 6
         Function evaluations: 14
         Gradient evaluations: 7

array([3.83746709])

Cuando no sabemos el intervalo del mínimo global podemos ocupar un método costoso que utiliza la fuerza bruta, en que se evalúa la función en cada punto

grid = (-10, 10, 0.1)
xmin_global = optimize.brute(f, (grid,))
xmin_global

array([-1.30641113])

Podemos encontrar un mínimo local (dentro de un intervalo), usando fminbound

xmin_local = optimize.fminbound(f, 0, 10)    
print(xmin_local)

3.8374671194983834

Para encontrar las raíces de una función, podemos utilizar fsolve. La raíz corresponde al punto donde $f(x)=0$.

root = optimize.fsolve(f, 1)  # our initial guess is 1
root

array([0.])

Si la función tiene más de una raíz, tenemos que cambiar el valor inicial para partir de un punto que nos lleve a la segunda (tercera…) solución

root2 = optimize.fsolve(f, -2.5)
root2

array([-2.47948183])

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, f(x), 'b-', label="f(x)")
xmins = np.array([xmin_global[0], xmin_local])
ax.plot(xmins, f(xmins), 'go', label="Minima")
roots = np.array([root, root2])
ax.plot(roots, f(roots), 'kv', label="Roots")
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('f(x)')

Text(0, 0.5, 'f(x)')

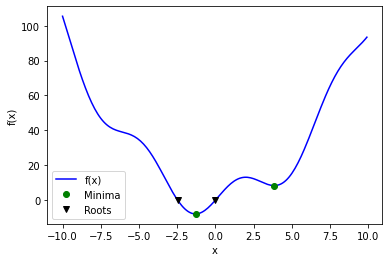
Supongamos que $f$ tiene un poco de ruido

xdata = np.linspace(-10, 10, num=20)
ydata = f(xdata) + np.random.randn(xdata.size)


plt.plot(x, f(x), 'b-', label="f(x)")
plt.plot(xdata, ydata, color="red")

[<matplotlib.lines.Line2D at 0x7f6a1004aa00>]

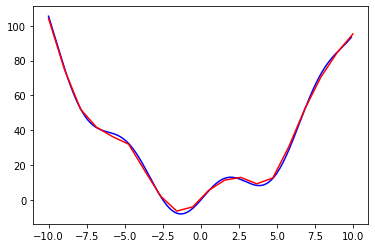
La forma funcional original es $$f(x) = x^2 + 10*sin(x)$$

Entonces podemos generalizar mediante

\[f(x,a,b) = a*x^2 + b*sin(x)\]

Mediante curve_fit() podemos encontrar los valores de a y b.

def f2(x,a ,b):
    return a*x**2 + b**np.sin(x)

#Valor inicial
guess = [2,2]

#curve_fit(f, xdata, ydata, valor inicial)
params, params_covariance = optimize.curve_fit(f2, xdata, ydata, guess)

#retorna: 
#1) Valores óptimos que minimizan f(xdata) - ydata
#2) Covarianza estimada de valores óptimos
params

array([ 0.95241285, 11.53081666])

fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, f(x), 'b-', label="f(x)")
ax.plot(x, f2(x, *params), 'r--', label="Curve fit result")

xmins = np.array([xmin_global[0], xmin_local])
ax.plot(xmins, f(xmins), 'go', label="Minima")
roots = np.array([root, root2])
ax.plot(roots, f(roots), 'kv', label="Roots")
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('f(x)')

Text(0, 0.5, 'f(x)')

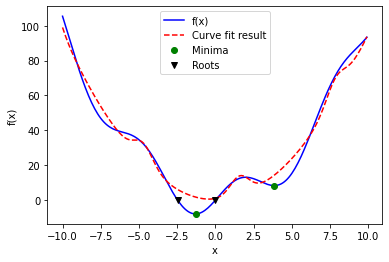
Estadísticas y números aleatorios¶

Podemos ocupar el módulo scipy.stats tiene potentes herramientas estadísticas y probabilísticas.

Para la generación de procesos aleatorios podemos ocupar numpy.random

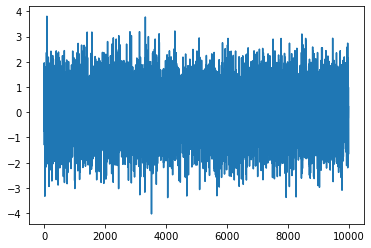
a = np.random.normal(size=10_000)
plt.plot(a)

[<matplotlib.lines.Line2D at 0x7f6a0ffa56a0>]

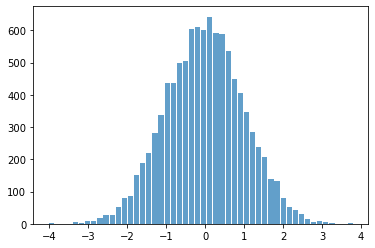
plt.hist(x=a, bins=50, alpha=0.7, rwidth=0.85);

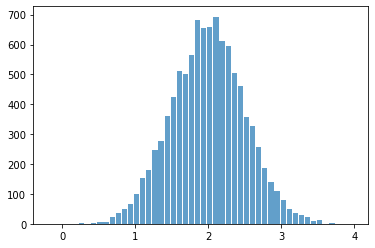
mu, sigma = 2, 0.5
s = np.random.normal(mu, sigma, 10000)
plt.hist(x=s, bins=50, alpha=0.7, rwidth=0.85);

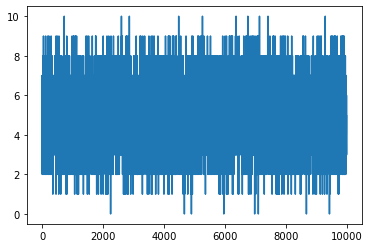
n, p = 10, .5 
s = np.random.binomial(n, p, 10_000)
plt.plot(s)
#Resultado de tirar una moneda 10 veces, testeado 10_000 veces

[<matplotlib.lines.Line2D at 0x7f6a0f8fa4c0>]

plt.hist(x=s, bins=10, alpha=0.7, rwidth=0.85);

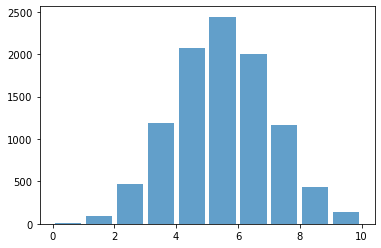
sum(np.random.binomial(2, 0.1, 20000) == 0)/20000
#COrremos el modelo 20_000 veces, y vemos el resultado de la probabilidad que se generen valores igual a cero

0.81165

Probability density function for norm: $$f(x) = \frac{exp(-x^2/2)}{\sqrt{2\pi}}$$

#Probability density function
from scipy.stats import norm

#Obtener momentos
x = np.linspace(-3, 3, 1000)
pdf = norm.pdf(x)
plt.plot(x, pdf)

[<matplotlib.lines.Line2D at 0x7f6a0e9992b0>]

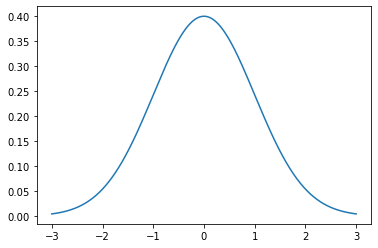
cdf = norm.cdf(x)
plt.plot(x, cdf)

[<matplotlib.lines.Line2D at 0x7f6a0e971d30>]

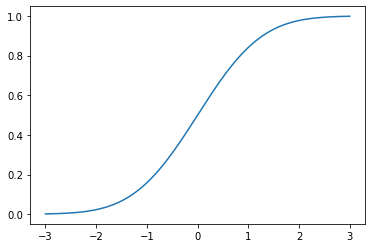
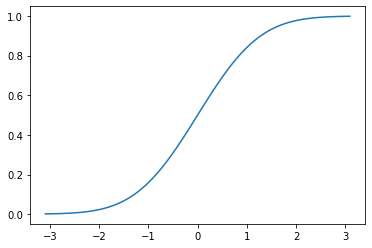
cdf = np.linspace(0, 1, 1000)
ppf = norm.ppf(cdf)
plt.plot(ppf, cdf)

[<matplotlib.lines.Line2D at 0x7f6a0e92e910>]

Interpolación¶

Cuando tenemos datos y no conocemos su forma funcional, podemos realizar una aproximación mediante una interpolación. Esto consiste en evaluar los puntos y obtener una aproximación de la función. En simple, nos permite mediante un set de valores discretos tener una función que nos permite tener un espacio continuo

Para esto podemos ocupar el módulo interpolate

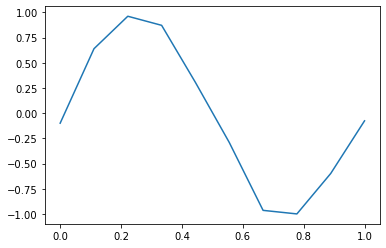
#Creamos datos experimentales: ejm similar a una función seno
x = np.linspace(0, 1, 10)
noise = (np.random.random(10)*2 - 1) * 1e-1
valores = np.sin(2 * np.pi * x) + noise

plt.plot(x, valores);

from scipy.interpolate import interp1d

#Creamos valores nuevos
val_nuevos = np.linspace(0, 1, 50)
#Interpolación lineal
linear_interp = interp1d(x, valores)
linear_results = linear_interp(val_nuevos)
#Interpolación cúbica
cubic_interp = interp1d(x, valores, kind='cubic')
cubic_results = cubic_interp(val_nuevos)

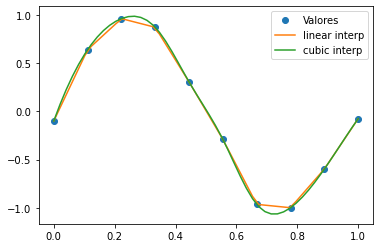
plt.plot(x, valores, 'o', ms=6, label='Valores')
plt.plot(val_nuevos, linear_results, label='linear interp')
plt.plot(val_nuevos, cubic_results, label='cubic interp')
plt.legend()
plt.show()

Actividad¶

Obtenga la inversa de una matriz a del tipo $$a = \left[ \begin{array}{ccc} 3 & 2 & 0 \\ 1 & -1 & 0 \\ 0 & 5 & 1 \\ \end{array}\right]$$

inv_a = linalg.inv(a)

Resuelva el sistema $a*x = b$, donde $$b = \left[ \begin{array}{c} 2 \\ 4 \\ -1 \\ \end{array}\right]$$

import numpy as np
a = np.array([[3, 2, 0], [1, -1, 0], [0, 5, 1]])

b = np.array([2, 4, -1])

from scipy import linalg

x = linalg.solve(a, b)
x

array([ 2., -2.,  9.])

Si compara $x = a^{-1}*b$ usando 1) con el resultado de 2), son iguales?

inv_a @ b

array([ 2., -2.,  9.])

4.

4.0

b = 10;

def f(X): 
    return (X[0]-1)**2 + b*(X[1]-X[0]**2)**2

# Initialize figure 
import matplotlib.pyplot as plt
figRos = plt.figure(figsize=(12, 7))
axRos = figRos.gca(projection='3d')

# Evaluate function
X = np.arange(-2, 2, 0.15)
Y = np.arange(-1, 3, 0.15)
X, Y = np.meshgrid(X, Y)
Z = f([X,Y])

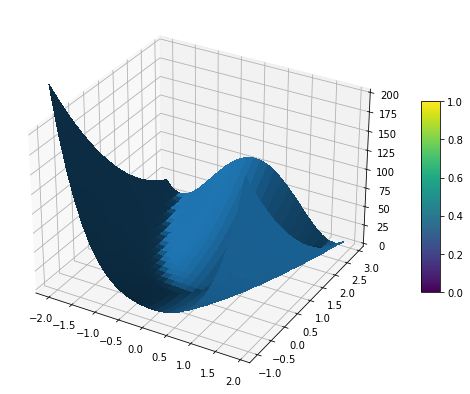
# Plot the surface
surf = axRos.plot_surface(X, Y, Z,
                       linewidth=0, antialiased=False)
axRos.set_zlim(0, 200)
figRos.colorbar(surf, shrink=0.5, aspect=10)
plt.show()

from scipy.optimize import least_squares
input = np.array([2, 2])
res = least_squares(f, input)
res

 active_mask: array([0., 0.])
        cost: 0.0021748096395843544
         fun: array([0.06595164])
        grad: array([-0.00102082,  0.01379367])
         jac: array([[-0.01547836,  0.20914825]])
     message: 'The maximum number of function evaluations is exceeded.'
        nfev: 200
        njev: 189
  optimality: 0.013793670721659863
      status: 0
     success: False
           x: array([1.25467248, 1.58466043])

Introducción a python